
我々の目標は、肉眼では困難あるいは不可能な動画の時間的変化を明らかにし、それを分かりやすく表示することである。「オイラービデオ拡大」と名付けたこの手法は、標準的な動画シーケンスを入力として、空間分解を行い、フレームに時間フィルタリングを適用する。得られた信号を増幅することで、隠れた情報を明らかにする。この手法を用いることで、顔面を流れる血流を可視化できるだけでなく、微細な動きも増幅して明らかにすることができる。この技術はリアルタイムで実行でき、ユーザーが選択した時間周波数で発生する現象を表示することができる。
人間の視覚システムは時空間感度に限界があるが、その限界以下の信号も有益な情報となり得る。例えば、人間の肌の色は血液循環によってわずかに変化する。この変化は肉眼では見えないが、脈拍数を抽出するために利用できる[Verkruysse et al. 2008; Poh et al. 2010; Philips 2011]。同様に、空間振幅の小さい動きは人間には見えにくい、あるいは見えないが、拡大することで興味深い機械的挙動を明らかにすることができる[Liu et al. 2005]。これらのツールの成功は、動画内の目に見えない信号を明らかにするための新しい技術の開発を促進している。本稿では、動画の空間処理と時間処理を組み合わせることで、我々の周りの世界の重要な側面を明らかにする微妙な変化を増幅できることを示す。
我々の基本的なアプローチは、任意の空間位置(ピクセル)における色情報の時系列を考慮し、特定の時間周波数帯域における変動を増幅することである。例えば図1では、人間の心拍数を含む可能性のある時間周波数帯域を自動的に選択し、増幅している。この増幅により、顔面を流れる血液の赤みの変化が明らかになる。この応用では、このような微細な入力信号をカメラセンサーと量子化ノイズよりも高いレベルにするために、低空間周波数帯域に時間フィルタリング(空間プーリング)を適用する必要がある。

図1:オイラービデオ拡大フレームワークを用いて人間の脈拍を可視化した例。(a) 元のビデオシーケンス(顔)の4フレーム。(b) 同じ4フレームで被験者の脈拍信号を増幅したもの。(c) 入力ビデオ(上)と出力ビデオ(下)の垂直走査線を時間経過に沿ってプロットしたもの。周期的な色の変化が増幅される様子を示している。入力シーケンスでは信号は目立たないが、拡大されたシーケンスでは変化が明瞭に確認できる。シーケンス全体は補足ビデオで見ることができる。
我々の時間フィルタリング手法は、色の変化を増幅するだけでなく、低振幅の動きも明らかにすることができる。例えば、補足動画では、呼吸する赤ちゃんの胸の周りの微妙な動きを強調できることを示している。時間フィルタリングが動画内の空間的な動きとどのように相互作用するかを説明する数学的解析を提供する。この解析は、オプティカルフローの定式化で使用される輝度一定仮定に関連する線形近似に基づいている。また、この近似が成立する条件も導出する。これにより、特徴追跡や動き推定を行わずに動きを拡大するマルチスケールアプローチが可能になる。
動画内の知覚できない動きを明らかにする試みはこれまでにも行われてきた。[Liu et al. 2005]は、微細な動きを分析・増幅し、本来であれば目に見えない変形を視覚化した。[Wang et al. 2006]は、Cartoon Animation Filterを用いて、知覚的に魅力的な動きの誇張表現を提案している。これらのアプローチは、粒子の軌跡を時間経過に沿って追跡する流体力学を参考に、ラグランジュの視点に基づいている。そのため、特に遮蔽境界や複雑な動きの領域では、アーティファクトのない画像を作成するのが困難である。さらに、Liu et al. [2005]は、高品質な合成を行うには、動きのセグメンテーションや画像のインペインティングなどの追加技術が必要であることを示している。これにより、アルゴリズムの複雑さがさらに増す。
対照的に、我々はオイラーの視点から着想を得ている。オイラーの視点では、流体のボクセルの圧力や速度といった特性が時間とともに変化する。我々の場合、空間的にマルチスケールな方法で、ピクセル値の時間的変化を研究し、増幅する。動きの拡大に対する我々のオイラーのアプローチでは、動きを明示的に推定するのではなく、固定位置における時間的な色の変化を増幅することで動きを誇張する。我々は、オプティカルフローアルゴリズムの基礎となる微分近似法(Lucas and Kanade 1981; Horn and Schunck 1981)と同じ手法を採用している。
時間処理は、これまで目に見えない信号の抽出[Poh et al. 2010]や動きの滑らかさの実現[Fuchs et al. 2010]に利用されてきた。例えば、Poh et al. [2010]は、人間の目には通常見えない肌の色の時間的変化に基づいて、顔の動画から心拍数を抽出した。彼らは単一の数値の抽出に焦点を当てていたが、我々は局所的な空間プーリングとバンドパスフィルタリングを用いて、脈拍に対応する信号を抽出し、視覚的に明らかにする。このプライマルドメイン解析により、顔の各部位における脈拍信号を増幅し、視覚化することができる。これは、例えば顔面血流の非対称性が動脈疾患の症状である可能性があるなど、医療分野における重要なモニタリングおよび診断アプリケーションの可能性を秘めている。
Fuchsら[2010]は、ピクセル単位の時間フィルタを用いて、動画における動きの時間的エイリアシングを抑制している。彼らは動きのハイパスフィルタリングについても議論しているが、主に非フォトリアリスティックな効果や大きな動きを対象としている(論文の図11)。これに対し、本手法は、マルチスケールアプローチを用いて、知覚できない動きを可視化することを目指している。本手法を理論的に分析し、小さな動きにのみ適用できることを示す。
本論文では、いくつかの貢献を行う。まず、標準的な単眼ビデオシーケンスのオイラー空間時間処理によって、動的環境におけるほぼ目に見えない変化を明らかにできることを実証する。さらに、様々なアプリケーションに適した増幅値の範囲において、自然なビデオにおける動きを増幅するために明示的な動き推定は必要ない。我々のアプローチは堅牢で、リアルタイムで実行される。次に、時間フィルタリングと空間動きの関係を分析し、我々の手法が小さな変位と低い空間周波数に最適であることを示す。最後に、空間動きと純粋に時間的な変化(例えば心拍)の両方を増幅するために使用できる単一のフレームワークを提示し、特定の時間周波数を増幅するように調整することもできる。これはラグランジュ法ではサポートされていない機能である。最後に、様々なノイズ条件下でのオイラーとラグランジュの動き拡大アプローチを解析的かつ経験的に比較する。我々のアプローチを実証するために、我々の手法によってシーン内の微妙な変化が可視化されるいくつかの例を示す。
我々のアプローチは、空間処理と時間処理を組み合わせることで、ビデオ内の微妙な時間的変化を強調する。そのプロセスを図 2 に示す。まず、ビデオ シーケンスを異なる空間周波数帯域に分解する。これらの帯域は、(a) 異なる信号対雑音比を示す場合、または (b) 動きの拡大に使用した線形近似が成り立たない空間周波数を含む場合 (セクション 3) があるため、異なって拡大される可能性がある。後者の場合、アーティファクトを抑制するためにこれらの帯域の増幅率を下げる。空間処理の目的が、複数のピクセルをプールして時間的な信号対雑音比を高めることだけである場合は、ビデオのフレームを空間的にローパス フィルタ処理し、計算効率を高めるためにダウンサンプリングする。ただし、通常は完全なラプラシアン ピラミッドを計算する [Burt and Adelson 1983]。
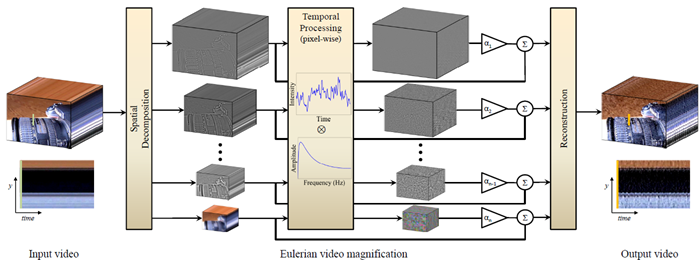
図2:オイラービデオ拡大フレームワークの概要。このシステムはまず、入力ビデオシーケンスを異なる空間周波数帯域に分解し、すべての帯域に同じ時間フィルタを適用する。フィルタリングされた空間帯域は、所定の係数 \(\alpha\) で増幅され、元の信号に再び加算され、合成されて出力ビデオが生成される。時間フィルタと増幅係数の選択は、さまざまなアプリケーションに対応するように調整できる。例えば、このシステムを使用して、デジタル一眼レフカメラの連写中にミラーが反転することで生じる、目に見えない動きを明らかにしている(camera; 全シーケンスは補足ビデオで見ることができる)。
次に、各空間バンドに対して時間処理を実行する。周波数バンド内のピクセルの値に対応する時系列を考慮し、バンドパス フィルターを適用して対象の周波数バンドを抽出する。たとえば、脈拍を拡大する場合、1 分あたり 24 ~ 240 拍に対応する 0.4 ~ 4 Hz 内の周波数を選択する。脈拍数を抽出できれば、その値の周りの狭いバンドを使用できる。時間処理は、すべての空間レベルと、各レベル内のすべてのピクセルに対して均一である。次に、抽出したバンドパス信号に拡大係数 \(\alpha\) を掛ける。この係数はユーザーが指定でき、セクション 3.2 のガイドラインに従って自動的に減衰される場合がある。使用可能な時間フィルターについては、セクション 4 で説明する。次に、拡大された信号を元の信号に追加し、空間ピラミッドを縮小して最終出力を取得する。自然なビデオは空間的にも時間的にも滑らかであり、フィルタリングはピクセル上で均一に実行されるため、我々の方法は結果の空間的および時間的な一貫性を暗黙的に維持する。
我々の処理は、ラグランジュ法[Liu et al. 2005;Wang et al. 2006]のように動きを追跡しないにもかかわらず、小さな動きを増幅することができる。本節では、オプティカルフロー解析で一般的に用いられる一次テイラー級数展開[Lucas and Kanade 1981; Horn and Schunck 1981]を用いた解析を用いて、時間的処理がどのように動きの増幅を生み出すかを示す。
時間処理と運きの拡大の関係を説明するために、並進運動する1次元信号の単純な例を考察する。この解析は、2次元における局所的な並進運動にそのまま一般化できる。
\(I(x, t)\) を位置 \(x\)、時刻 \(t\) における画像の強度とする。画像は並進運動をするため、観測された強度は変位関数 \(δ(t)\) に関して、\(I(x, t) = f(x + δ(t)), I(x, 0) = f(x)\) と表すことができる。運き拡大の目的は、信号を合成することである。 \[ \hat{I}(x,t)=f\left(x+(1+\alpha)\delta(t)\right) \tag{1} \] ある増幅係数 \(\alpha\) に対して。
像が一次テイラー展開で近似できると仮定して、時刻 \(t\) における像 \(f(x +\delta(t))\) を \(x\) に関する一次テイラー展開で次のように書き表す。 \[ I(x,t)\approx f(x)+\delta(t)\frac{\partial f(x)}{\partial x} \tag{2} \] \(B(x,t)\) を、あらゆる位置 \(x\) において \(I(x,t)\) に広帯域時間バンドパスフィルタを適用した結果とする(式2の \(f(x)\) を除くすべてを除去)。ここでは、動き信号 \(\delta(t)\) が時間バンドパスフィルタの通過帯域内にあると仮定する(この仮定は後で緩和する)。すると、 \[ B(x,t)=\delta(t)\frac{\partial f(x)}{\partial x} \tag{3} \] 我々のプロセスでは、そのバンドパス信号を \(\alpha\) だけ増幅し、それを \(I(x, t)\) に加算することで、処理された信号が得られる。 \[ \tilde{I}(x,t)=I(x,t)+\alpha B(x,t) \tag{4} \] 式2、3、4を組み合わせて以下を得る。 \[ \tilde{I}(x,t)\approx f(x)+(1+\alpha)\delta(t)\frac{\partial f(x)}{\partial x} \tag{5} \] 増幅された大きな摂動 \((1+\alpha)\delta(t)\) に対して一次テイラー展開が成り立つと仮定すると、時間的にバンドパスされた信号の増幅と動きの拡大を関連付けることができる。処理された出力は単純に \[ \tilde{I}(x,t)\approx f(x+(1+\alpha)\delta(t)) \tag{6} \] これは、処理によって動きが拡大されていることを示している。つまり、時刻 \(t\) における局所画像 \(f(x)\) の空間変位 \(\delta(t)\) が、\((1+\alpha)\) の大きさに増幅されているのである。
このプロセスは、図3に単一の正弦波について示されている。低周波の余弦波と比較的小さな変位 \(\delta(t)\) の場合、1次テイラー級数展開は、時刻 \(t + 1\) における変換信号の良い近似値となる。時間信号を増幅し、それを \(I(x,t)\) に加算すると、変換された波は \((1+\alpha)\delta\) で近似される。
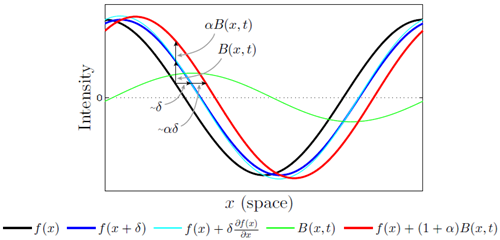
図3:時間フィルタリングは空間移動を近似できる。この効果はここでは1次元信号で示されているが、2次元信号にも同様に適用される。入力信号は2つの時点、すなわち時刻 \(t\) における \(I(x, t) = f(x)\) と時刻 \(t + 1\) における \(I(x, t + 1) = f(x +\delta)\) で示されている。\(I(x, t + 1)\)の \(x\) に関する1次テイラー展開は、移動後の信号を適切に近似する。時間バンドパスは増幅され、元の信号に追加されることで、より大きな移動が生成される。この例では \(\alpha = 1\) であり、動きを100%拡大し、時間フィルタは2つの曲線を減算する有限差分フィルタである。
完全を期すために、\(\delta(t)\) が時間フィルタの通過帯域内に完全に収まらない、より一般的なケースに戻ろう。この場合、\(k\) でインデックス付けされた \(\delta_k(t)\) は、\(\delta(t)\) の異なる時間スペクトル成分を表す。各 \(\delta_k(t)\) は、時間フィルタによって係数 \(\gamma_k\) で減衰される。これにより、帯域通過信号が生成される。 \[ B(x,t)=\sum_k \gamma_k\delta_k(t)\frac{\partial f(x)}{\partial x} \tag{7} \] (式3と比較のこと)。式4の乗算により、この時間的な周波数依存減衰は、周波数依存の動き拡大係数、\(\alpha_k = \gamma_k\alpha\) として等価的に解釈でき、動き拡大出力が得られる。 \[ \tilde{I}(x,t)\approx f(x+\sum_k(1+\alpha_k)\delta_k(t)) \tag{8} \] 結果は線形解析で予想される通りである。動き信号のスペクトル成分の変調は、動き信号の各時間サブバンド \(\delta_k\) に対する動き増幅係数 \(\alpha_k\) の変調係数になる。
実際には、3.1節の仮定は滑らかな画像と小さな動きに対して成り立つ。急速に変化する画像関数(すなわち、高い空間周波数)\(f(x)\) の場合、一次テイラー級数近似は、大きな摂動値 \(1+\alpha\delta(t)\) に対して不正確になる。摂動値は、倍率\(\alpha\) と動き \(\delta(t)\) の両方が大きくなるにつれて大きくなる。図4と図5は、高周波、大きな増幅率、そして大きな動きが、動き増幅された正弦波信号に与える影響を示している。
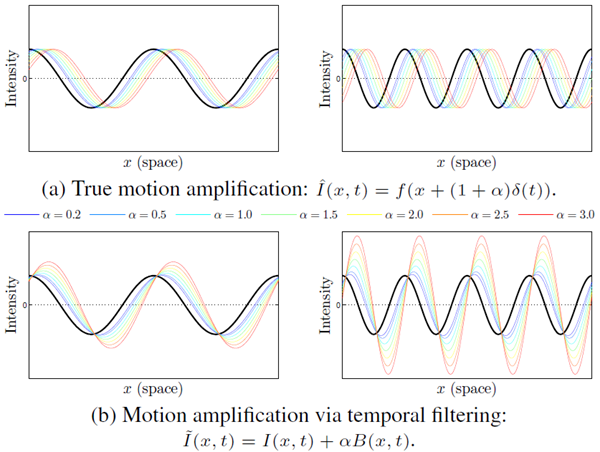
図 4: 異なる空間周波数と \(\alpha\) 値での 1D 信号の動きの増幅の図解。左側の画像では、 \(\lambda = 2\pi\) および \(\delta(1) = \frac{\pi}{8}\) が真の移動である。右側の画像では、 \(\lambda = \pi\) および \(\delta(1) = \frac{\pi}{8}\) である。(a) 時刻 \(t = 1\) における \(I(x, 0)\) の \((1 +\alpha)\delta(t)\) による真の変位。青 (小さい増幅率) から赤 (大きい増幅率) に色分けされている。(b) フィルターによって生成された増幅された変位。色は (a) で正しくシフトされた信号に対応している。式14 を参照すると、各プロットの赤い (右端の) 曲線は、左側のプロットでは \((1 +\alpha)\delta(t) =\frac{\lambda}{4}\) に対応し、右側のプロットでは \((1+\alpha)\delta(t) = \frac{\lambda}{2}\) に対応しており、それぞれ \((1 +\alpha) の境界を \(2\) 倍と \(4\) 倍超えたことで、動きの拡大で軽度、次に重度のアーティファクトが発生したことを示している。
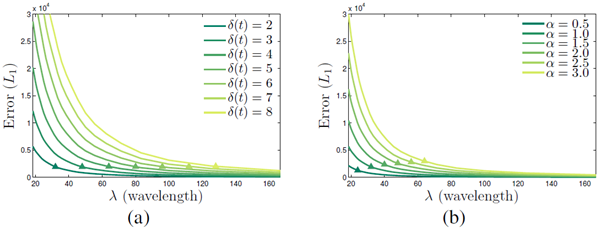
図5: 真の動き増幅信号(図4(a))と時間フィルタリングされた結果(図4(b))間の\(L_1\)ノルムとして計算されたモーション増幅誤差(波長の関数)。\(\delta(t)\)(a)と\(\alpha\)(b)の異なる値について。(a)では\(\alpha = 1\)に固定し、(b)では\(\delta(t) = 2\)に固定している。各曲線上のマーカーは、導出されたカットオフポイント\((1 +\alpha)\delta(t) = \frac{\lambda}{8}\)(式14)を表している。
空間周波数 \(\omega\) の関数として、観測された動き \(\delta(t)\) が与えられた場合に、動きの増幅係数 \(\alpha\) をどの程度まで大きくできるかについての指針を導くことができる。処理された信号 \(\tilde{I}(x,t)\) が真の拡大された動き \(\hat{I}(x,t)\) にほぼ等しくなるようにするために、以下の条件を求める。 \[ \begin{align} \tilde{I}(x,t) &\approx \hat{I}(x,t) \\ \\ \Rightarrow f(x)+(1+\alpha)\delta(t)\frac{\partial f(x)}{\partial x} &\approx f(x+(1+\alpha)\delta(t)) \tag{9} \end{align} \] 空間周波数 \(\omega\) に対して\(f(x) = cos(\omega x)\) とし、\(\beta=1+\alpha\) と表そう。我々は以下を要求する。 \[ \cos(\omega x)-\beta\omega\delta(t)\sin(\omega x)\approx \cos(\omega x+\beta\omega\delta(t)) \tag{10} \] 余弦の加法則を用いると、 \[ \cos(\omega x)-\beta\omega\delta(t)\sin(\omega x)=\cos(\omega x)\cos(\beta\omega\delta(t))-\sin(\omega x)\sin(\beta\omega\delta(t)) \tag{11} \] したがって、おおよそ次の式が成り立つ。 \[ \begin{align} \cos(\beta\omega\delta(t)) &\approx 1 \tag{12} \\ \\ \sin(\beta\omega\delta(t)) &\approx \beta\delta(t)\omega \tag{13} \end{align} \] 式(12)および式(13)の小角近似は、\(\beta\omega\delta(t)\leq \frac{\pi}{4}\)の10%以内で成立する(正弦項が主要近似であり、\(sin(\frac{\pi}{4})=0.9\frac{\pi}{4}\))。移動信号の空間波長\(\lambda=\frac{2\pi}{\omega}\)に関して、これは以下の式で表される。 \[ (1+\alpha)\delta(t)\lt \frac{\lambda}{8} \tag{14} \] 上記の式14は、我々が求めるガイドラインを提供し、与えられたビデオモーション \(\delta(t)\) と画像構造の空間波長 \(\lambda\) の正確なモーション拡大と互換性のある、最大のモーション増幅係数 \(\lambda\) を与える。図4 (b)は、式14の制限を超えてブーストした場合の正弦波のモーション拡大誤差を示している。一部のビデオでは、近似限界を超えることが知覚的に好ましい場合があり、\(\lambda\) カットオフはマルチスケール処理においてユーザーが変更可能なパラメータとして残す。
セクション3.2の分析では、スケールを変化させるプロセスが提案されている。これは、特定の空間周波数帯域に対して指定された \(\alpha\) 拡大係数を適用し、増幅によって望ましくないアーティファクトが生じる高空間周波数帯域(式14から求められるか、ユーザーが指定する)に対してはスケールを縮小するというものである。図6は、このような \(\alpha\) の変調方式を示している。高空間周波数帯域(鋭いエッジ)は、一般的に低周波数帯域よりも増幅度が低くなるが、結果として得られる動画には、知覚的に魅力的な拡大された動きが含まれていることがわかった。この効果は、Freemanら[1991]の以前の研究でも利用され、静止画像に動きがあるような錯覚を作り出すために用いられた。
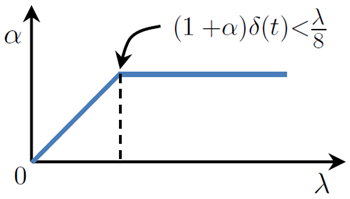
図6: 運き動を増幅するための増幅係数\(\alpha\)と空間波長\(\lambda\)の関数。増幅係数は、導出した境界(式14)内の空間帯域では\(\alpha\)に固定され、より高い空間周波数では線形に減衰する。
結果は、6コアプロセッサと32GB RAMを搭載したマシン上で、最適化されていないMATLABコードを使用して生成された。動画1本あたりの計算時間は数分程度だった。動画ピラミッドの構築には、サイズ5の分離型二項フィルターを使用した。また、ライブ動画フィードから微妙な変化をリアルタイムで観察できるプロトタイプアプリケーションも構築した。これは、時間的な変化を観察するための顕微鏡として機能する。このアプリケーションはC++で実装されており、完全にCPUベースで動作し、標準的なノートパソコンで640×480の動画を毎秒45フレームで処理する。GPUを利用することでさらに高速化できる。アプリケーションのデモは付属のビデオで見ることができる。コードはプロジェクトのWebページで入手できる。
入力ビデオをオイラービデオ拡大法で処理するには、ユーザーは4つの手順を実行する必要がある。(1) 時間バンドパス フィルターを選択する。(2) 増幅係数 \(\alpha\) を選択する。(3) 空間周波数カットオフ (空間波長 \(\lambda_c\) で指定) を選択する。このカットオフを超えると、\(\alpha\) の減衰バージョンが使用される。(4) \(\alpha\) の減衰形式を選択する。\(\lambda < \lambda_c\) のすべての場合に \(\alpha\) を 0 に強制するか、\(\alpha\) を線形に 0 に縮小するかを選択する。対象となる周波数帯域は自動的に選択される場合もあるが、多くの場合、ユーザーがアプリケーションに応じて周波数帯域を制御できることが重要である。我々のリアルタイム アプリケーションでは、増幅係数とカットオフ周波数はすべてユーザーがカスタマイズできる。
まず、増幅したい動きや信号を抽出するために時間バンドパス フィルターを選択する (上記の手順 1)。フィルターの選択は、一般的にアプリケーションによって異なる。動きの増幅には、広い通過帯域を持つフィルターが適している。血流の色増幅には、狭い通過帯域の方がノイズの少ない結果になる。図 9 は、この論文で使用されているいくつかの時間フィルターの周波数応答を示している。色増幅には、鋭いカットオフ周波数の通過帯域を持つ理想的なバンドパス フィルターを使用する。低次 IIR フィルターは、色増幅と動きの増幅の両方に役立ち、リアルタイム実装にも便利である。通常、カットオフ周波数が \(\omega_l\) と \(\omega_h\) の 2 つの 1 次ローパス IIR フィルターを使用して、IIR バンドパス フィルターを構築する。
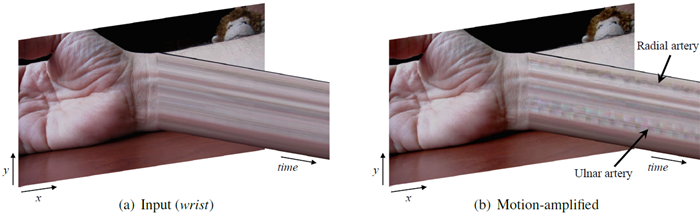
図 7: 血流によって生じる血管の微妙な動きを増幅するために使用されるオイラービデオ拡大。このビデオでは、時間フィルターを心拍数 (0.88 Hz (53 bpm)) を含む周波数帯域に調整し、増幅係数を \(\alpha = 10\) に設定した。無関係なオブジェクトの動きの拡大を減らすために、ユーザー指定のマスクを適用して手首の近くの領域のみを増幅した。橈骨動脈と尺骨動脈の動きは、標準的なコンパクトカメラで撮影した入力ビデオ (a) ではほとんど見えないが、動きが拡大された出力 (b) でははるかに顕著である。脈打つ動脈の動きは、手首の空間的および時間的な Y T スライス (a) と (b) を観察すると、よりはっきりと見える。手首の完全なシーケンスは、補足ビデオで見ることができる。

図8: 我々の技術を実証する追加ビデオの代表的なフレーム。ビデオは付属ビデオとプロジェクトのウェブページで見ることができる。
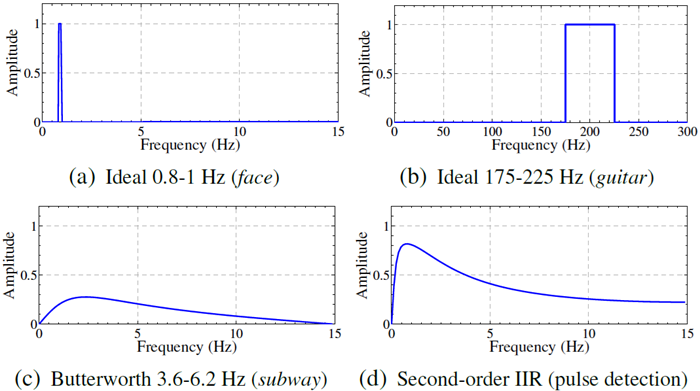
図9:本論文で使用した時間フィルタ。理想フィルタ(a)と(b)はDCTを用いて実装されている。バターワースフィルタ(c)は、ユーザ指定の周波数帯域を2次IIR構造に変換するために使用され、リアルタイムアプリケーションで使用されている。2次IIRフィルタ(d)もユーザ入力に対応している。これらの2次フィルタは、理想フィルタよりも広い通過帯域を持つ。
次に、必要な拡大値 \(\alpha\) と空間周波数カットオフ \(\lambda_c\) を選択する (手順 2 および 3)。式 14 はガイドとして使用できるが、実際には、さまざまな \(\alpha\) および \(\lambda_c\) 値を試して、目的の結果を得ることができる。ユーザーは、境界に違反する高い値を選択して、特定の動きや色の変化を誇張することができるが、その代償としてノイズが増えたり、アーティファクトが増えたりすることになる。場合によっては、各フレームの彩度成分を減衰させることで、色クリッピング アーティファクトに対処することができる。我々のアプローチでは、すべての処理を YIQ 空間で実行することでこれを実現する。ユーザーは、元の色空間に変換する前に、彩度成分 I と Q を減衰させることができる。
人間の脈拍の色増幅では、低空間周波数の変化を強調したいため、\(\lambda_c\) 未満の空間波長に対して \(\alpha = 0\) を強制的に適用することができる。動きのある動画の拡大では、\(\alpha\) に線形ランプ遷移を適用することができる(手順4)。
肌の色の異なる大人のビデオ 2 本と新生児のビデオ 1 本を使用して、色増幅の方法を評価した。顔色の明るい大人の被験者は face (図 1) に示され、顔色の暗い個人は face2 (図 8) に示されている。両方のビデオで、我々の目的は、血液が顔を流れるときに生じる色の変化を増幅することだった。face と face2 の両方で、ラプラシアン ピラミッドを適用し、最も細かい 2 つのレベルの \(\alpha\) を 0 に設定した。基本的に、量子化とノイズの両方を削減し、対象の微細な脈拍信号を増幅するために、各フレームをダウンサンプリングして空間ローパス フィルターを適用した。次に、各ビデオで、フレームの各シーケンスを、通過帯域が 0.83 Hz~1 Hz (50 bpm ~ 60 bpm) の理想的なバンドパス フィルターに通した。最後に、得られた空間ローパス信号に \(\alpha\approx 100\) と \(\lambda_c\approx 1000\) という大きな値を適用し、色の変化を可能な限り強調した。この信号を元の信号に再び加算することで、最終的な動画が作成された。心拍数の変化と顔面への血液の流れによって、緑から赤への周期的な変化が確認できる。
baby2は、マサチューセッツ州ウィンチェスター病院の保育部門で撮影された新生児の動画である。動画に加え、病院グレードのモニターから正解のバイタルサインを取得した。この情報を用いて、心拍数推定値の精度を確認し、本手法で抽出した色増幅信号が、モニターで測定された皮膚への血液灌流を光学的に測定する光電式容積脈波(PHPT)と一致することを検証した。
動きの拡大に対する我々の手法を評価するために、face (図 1)、sim4 (図 10)、wrist (図 7)、camera (図2)、face2、guitar、baby、subway、shadow、baby2 (図 8) といういくつかの異なるビデオを使用した。すべてのビデオで、空間フィルタリングに標準のラプラシアン ピラミッドを使用した。特定の時間周波数で動きを強調したいビデオ (sim4 やguitarなど) では、理想的なバンドパス フィルターを使用した。sim4 とguitarでは、対象オブジェクトの振動周波数に調整されたバンドパス フィルターを使用することで、特定の領域またはギターの弦の動きを選択的に増幅することができた。これらの効果は補足ビデオで確認できる。本稿で説明したすべてのビデオで使用された \(\alpha\) と \(\lambda_c\) の値を表 1 に示す。

図10:合成シーケンス(左はsim4)における選択的な動きの増幅。ビデオシーケンスには、入力フレームに示されているように、異なる時間周波数で振動するブロブが含まれている。1~3Hzの理想的な時間バンドパスフィルターを用いて、指定された通過帯域内で発生する動きのみを増幅する手法を適用する。(b)は、結果のビデオから抽出した時空間スライスを示しており、異なる時間周波数と、2Hzで振動するブロブの増幅された動きを示している。時空間処理はすべてのピクセルに均一に適用されていることに注意。シーケンス全体と結果は、補足ビデオで見ることができる。
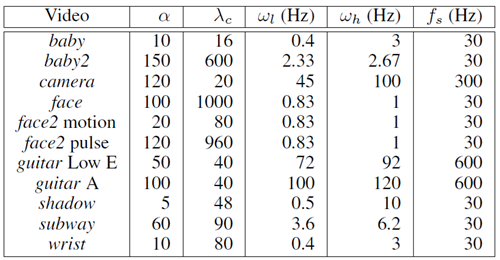
表1: 様々なビデオ出力を生成するために使用される\(\alpha,\lambda_c,\omega_l,\omega_h\)値の表。face2では、2つの異なるパラメータセットが使用されている。1つは脈拍を増幅するため、もう1つは動きを増幅するためである。guitar では、異なるカットオフ周波数と\((\alpha,\lambda_c\)の値を使用して、異なる振動するギターの弦を「選択」する。fs はカメラのフレームレートである。
広範囲かつ微細な動きを捉えたい動画では、より広い通過帯域を持つ時間フィルタを使用した。例えば、face2の動画では、緩やかなロールオフ領域を持つ2次IIRフィルタを使用した。時間フィルタを変更することで、肌の色の変化を増幅するのではなく、頭部の動きを拡大することができた。そこで、動きを拡大するために\(\alpha = 20, \lambda_c = 80\)を選択した。
広帯域時間フィルタを使用し、\(\alpha\) と \(\lambda_c\) を式 14 に従って設定することにより、camera や wrist のビデオのような微妙な動きを明らかにすることができる。camera のビデオでは、サンプリング レートが 300 Hz のカメラを使用して、1 秒あたり約 1 回の露出で写真を撮影しながら振動しているデジタル SLR カメラを記録した。SLR 内の可動ミラーによって引き起こされる振動は肉眼では見えないが、我々のアプローチによって明らかになった。反転するミラーによって引き起こされる振動を実際に増幅したことを確認するために、レーザー ポインターをカメラに固定し、光源から約 4 メートルの距離で現れるレーザー光のビデオを記録した。その距離では、レーザー光は各露出ごとに目に見えて振動し、振動は拡大された動きと同期していた。
我々の手法は、baby、face2、subway の動画に見られるように、目に見えるものの微妙な動きを誇張することもできる。subway の例では、効果を高め、アルゴリズムのアーティファクトを示すために、一次近似が成り立つ導出された境界を超えて動きを意図的に増幅した。我々の論文のほとんどの例には振動運動が含まれていることに注意。これは、そのような動きは一般に持続時間が長く、振幅が小さいためである。ただし、我々の手法は、時間バンドパスフィルタの通過帯域内にある限り、非周期的な動きを増幅するためにも使用できる。たとえば shadow では、15秒間にわたって直線的でありながら知覚できないほどに動く太陽の影の動画を処理する。拡大バージョンにより、この短い期間内でも変化を確認できる。
最後に、一部の動画には、増幅する必要のない、あるいは増幅しても知覚的に魅力のない時間的信号領域が含まれている場合がある。オイラー処理により、ユーザーは動画上で特定の領域をマークすることで、手動で拡大範囲を限定することができる(これは face と wrist に適用された)。
ノイズに対する感度
対象信号の振幅変動は、多くの場合、ビデオに内在するノイズよりもはるかに小さい。このような場合、ピクセル値を直接強調しても目的の信号は現れない。空間フィルタリングを用いることで、こうした微妙な信号を強調することができる。ただし、適用する空間フィルタの大きさが十分でない場合、対象信号は現れない(図11)。
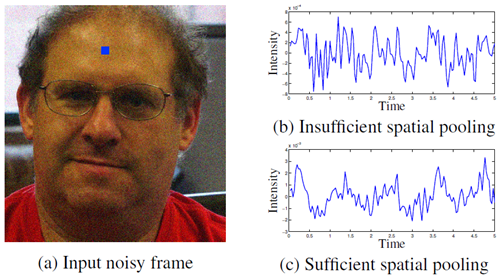
図 11: 適切な空間プーリングは、関心のある信号を明らかにするために不可欠である。(a) 顔のビデオ (図 1) のフレームに、白色ガウスノイズ (\(sigma = 0.1\) ピクセル) が追加された。右側には、入力フレームで青くマークされたピクセルの時間経過に伴う強度トレースが示されている。ここで、(b) は、(ノイズの多い) シーケンスを、元の顔のシーケンスの処理に使用したものと同じ空間フィルター (サイズ 20 の分離可能な二項フィルター) で処理したときに取得されたトレースを示しており、(c) は、式 15 の推定半径に応じて調整されたフィルター (サイズ 80 の二項フィルター) を使用したときのトレースを示している。ノイズ レベルが信号のパワーよりも高いため、(b) ではパルス信号は見えないが、(c) ではパルスがはっきりと見える (トレース内で周期的なピークが約 1 秒間隔で見られる)。
ノイズが平均 0 の白色ノイズであり、空間に関して広義の定常性を持つと仮定すると、空間ローパスフィルタリングは、ローパスフィルタの面積に応じてノイズの分散を低減することが示される。特定の信号(例えば face の脈拍信号)のパワーを高めるために、信号の空間特性を用いて空間フィルタのサイズを推定することができる。
ノイズパワーレベルを \(\sigma^2\) とし、空間周波数における信号パワーの事前分布を \(S(\lambda)\) とする。半径 \(r\) の空間ローパスフィルタを求める。このフィルタは、フィルタ処理後の周波数領域において信号パワーがノイズパワーよりも大きくなる。このようなフィルタの波長遮断はフィルタの半径 \(r\) に比例するため、信号事前分布は \(S(r)\) と表すことができる。ノイズパワー \(\sigma^2\) は、シーンの安定領域のピクセル値、グレーカード、または [Liu et al. 2006] のような手法を用いて推定できる。フィルタ処理後のノイズパワーレベル \(\sigma^{\prime 2}\) は \(r^2\) に反比例するため、次の式を \(r\) について解くことができる。 \[ S(r)=\sigma^{\prime 2}=k\frac{\sigma^2}{r^2} \tag{15} \] ここで、\(k\) はローパスフィルタの形状に依存する定数である。この式は、特定のノイズ電力レベルで信号を検出するために必要な空間フィルタのサイズを推定する。
オイラー処理 vs. ラグランジュ処理
2つの手法は動きに対して異なるアプローチを採用しているため(ラグランジュ手法は動きを明示的に追跡するが、我々のオイラー手法は追跡しない)、相補的な動きの領域に使用できる。ラグランジュ手法(例えば[Liu et al. 2005])は、細かい点の特徴の動きを強調し、大きな増幅率をサポートするのに優れているが、我々のオイラー手法は、より滑らかな構造と小さな増幅率に適している。なお、我々の手法は特定の種類の動きを想定していない。1次テイラー級数解析は、一般的な経路に沿った一般的な小さな2次元の動きに対して適用できる。
付録Aでは、ノイズに対する2つの手法の精度推定値をさらに導く。ラグランジュ誤差 \(\varepsilon_L\) (式29)とオイラー誤差 \(\varepsilon_E\) (式31)を比較すると、どちらの手法もノイズの時間特性 \(n_t\) に対して等しく敏感であることがわかる。一方、ラグランジュ過程は、動きの明示的な推定 (式27) により、ノイズの空間特性 \(n_x\) に比例した誤差項が追加される。一方、オイラー誤差は \(\alpha\) の2乗に比例して増加し、高空間周波数 \((I_{xx})\) に対してより敏感である。一般に、これは増幅が小さくノイズレベルが高い場合、ラグランジュ増幅よりもオイラー増幅の方が適していることを意味する。
この分析を、平均 0、標準偏差 \(\sigma\) の加法的な白色時空間ガウスノイズを加えた、時間的に 2 Hz、空間的に 0.1 ピクセルで振動する 2D コサインの合成シーケンスで検証した (図 12)。 結果は、導出によって予測された誤差とノイズ、および誤差と増幅の関係と一致している (図 12(b))。 オイラー手法がラグランジュの結果を上回る領域 (図 12(a) 左) も予想どおりである。ラグランジュ法は空間ノイズの増加に対してより敏感であるが、オイラー誤差はその影響をほとんど受けない (図 12(c))。 動き推定に使用されるさまざまな正則化スキーム (理論的に分析するのが難しい) によってラグランジュ誤差が軽減される可能性があるが、結果が大幅に変わることはなかった (図 12(a) 右)。一般的に、我々の実験では、小さな増幅においてはオイラーアプローチの方がパフォーマンスと効率のバランスが優れていることが示されている。自然な動画における両手法の比較は、プロジェクトのウェブページで見ることができる。
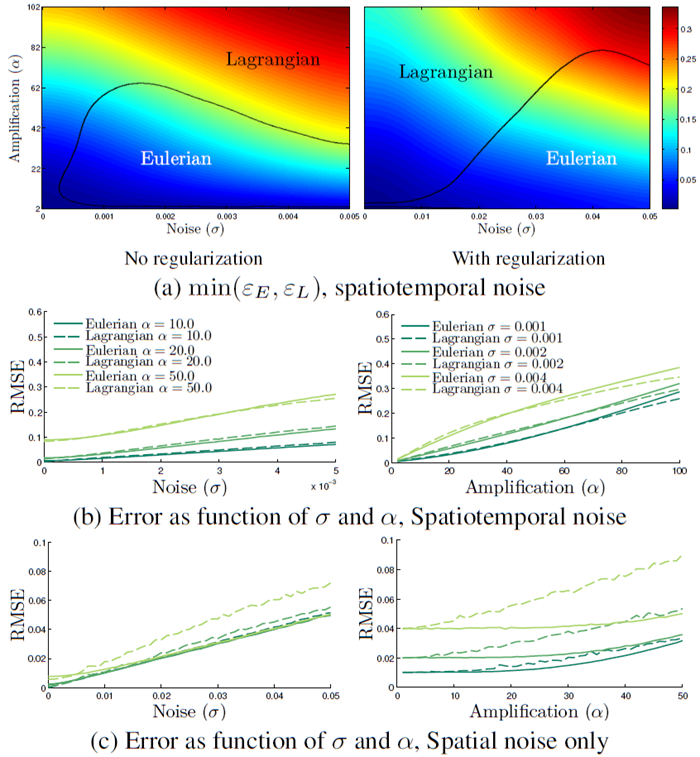
図 12: 加法性ノイズを含む合成シーケンスにおけるオイラーおよびラグランジュのモーション拡大の比較。(a) 最小誤差 \(min(\varepsilon_E,\varepsilon_L)\) は、各手法の結果と実際のモーション拡大シーケンスとの間の (フレーム単位の) RMSE として計算され、ノイズと増幅の関数として、青 (小さい誤差) から赤 (大きい誤差) に色分けされている。ラグランジュ法で空間正則化を行った場合 (左) と行わなかった場合 (右) を示している。黒い曲線は誤差面の交点を示し、重ね合わせたテキストは各領域で最もパフォーマンスの高い手法を示している。(b) 2 つの手法の RMSE をノイズ (左) と増幅 (右) の関数として示している。(d) (c) と同じであるが、空間ノイズのみを使用している。
動画を入力として、微妙な色の変化や知覚できない動きを誇張する、シンプルな手法を考案した。動きを増幅するために、本手法では特徴追跡やオプティカルフロー計算は行わず、時空間処理を用いて時間的な色の変化のみを拡大する。このオイラーベースの手法は、固定された空間領域内のピクセルを時間的に処理することで、実世界の動画における有益な信号を明らかにし、小さな動きを増幅することに成功した。
有益なフィードバックをいただいたGuha Balakrishnan氏、Steve Lewin-Berlin氏、Neal Wadhwa氏、そしてコメントをいただいたSIGGRAPH査読者の皆様に感謝申し上げます。オイラー解析とラグランジュ解析の比較について有益な議論をしていただいたCe Liu氏とDeqing Sun氏にも感謝申し上げます。また、新生児のビデオ収集にご協力いただいたDonna Brezinski博士、Karen McAlmon博士、そしてウィンチェスター病院のスタッフにも感謝申し上げます。本研究は、DARPA SCENICCプログラム、NSF CGV-1111415、およびQuanta Computerの支援を受けて実施されました。Michael Rubinsteinは、NVIDIA Graduate Fellowshipの支援を受けて実施されました。
空間的および時間的ノイズに対するオイラー方式およびラグランジュ方式の運き拡大の誤差の推定値を導く。簡略化のため、この導出は1次元で行ったが、2次元にも一般化できる。3.1節と同じ設定を用いる。
どちらの手法も、(1)に示すように、真の運き増幅されたシーケンス \(\hat{I}(x, t)\)を近似する。まず、クリーンな信号 \(I(x, t)\) におけるこれらの近似値の誤差を分析しよう。
ノイズなし
ラグランジュアプローチでは、動き増幅シーケンス \(\tilde{I}_L(x,t)\) は、推定された動き \(\tilde{\delta}(t)\) を参照フレーム \(I(x,0)\) に対して直接増幅することによって実現される。
\[
\tilde{I}_L(x,t)=I(x+(1+\alpha)\tilde{\delta}(t),0) \tag{16}
\]
最も単純な形では、\(\delta(t)\)を点ごとに推定することができる(空間正則化に関する議論についてはセクション5を参照)。
\[
\tilde{\delta}(t)=\frac{I_t(x,t)}{I_x(x,t)} \tag{17}
\]
ここで、\(I_x(x,t) = \partial I(x, t)/\partial x\) かつ \(I_t(x, t) = I(x, t)-I(x,0)\) である。以降、簡潔にするために、空間インデックス \((x)\) と時間インデックス \((t)\) は可能な限り省略する。
ラグランジュ解の誤差は、推定された動きの誤差によって直接決定され、これは輝度一定方程式の2次項として扱われる(ニュートン反復のため、光学フロー定式化では通常考慮されないが)。
\[
\begin{align}
I(x,t) \approx I(x,0)+\delta(t)I_x+\frac{1}{2}\delta^2(t)I_{xx} \\
\\
\Rightarrow \frac{I_t}{I_x}\approx \delta(t)+\frac{1}{2}\delta^2(t)I_{xx} \tag{18}
\end{align}
\]
推定された動き\(\tilde{\delta}(t)\)は、真の動き\(\delta(t)\)と次のように関係している。
\[
\tilde{\delta}(t)\approx\delta(t)+\frac{1}{2}\delta^2(t)I_{xx} \tag{19}
\]
(19)を(16)に代入し、\(I\) の \(x + (1 +\alpha)\delta(t)\) についてのテイラー展開を用いると、
\[
\tilde{I}_L(x,t)\approx I(x+(1+\alpha)\delta(t),0)+\frac{1}{2}(1+\alpha)\delta^2(t)I_{xx}I_x \tag{20}
\]
(1)から(20)を引くと、ラグランジュ運き拡大列の誤差\(\varepsilon_L\)は
\[
\varepsilon_L\approx \left|\frac{1}{2}(1+\alpha)\delta^2(t)I_{xx}I_x\right| \tag{21}
\]
我々のオイラー式アプローチでは、拡大された数列 \(\tilde{I}_E(x, t)\) は
\[
\begin{align}
\tilde{I}_E(x,t) &= I(x,t)+\alpha I_t(x,t) \\
\\
&=I(x,0)+(1+\alpha)I_t(x,t) \tag{22}
\end{align}
\]
(4)と同様に、2タップの時間フィルタを用いて \(I_t\)を計算する。(1)で定義した真の運き拡大列\(hat{I}\)をxについてテイラー展開すると、
\[
\hat{I}(x,t)\approx I(x,0)+(1+\alpha)\delta(t)I_x+\frac{1}{2}(1+\alpha)^2\delta^2(t)I_{xx} \tag{23}
\]
(18)式を用いて(23)式から(1)式を引くと、オイラー運き拡大列の誤差 \(\varepsilon_E\) は
\[
\varepsilon_E\approx\left|\frac{1}{2}(1+\alpha)^2\delta^2(t)I_{xx}-\frac{1}{2}(1+\alpha)\delta^2(t)I_{xx}I_x\right| \tag{24}
\]
ノイズあり
\(I^\prime(x, t)\) をノイズ信号とする。
\[
I^\prime(x,t)=I(x,t)+n(x,t) \tag{25}
\]
加法ノイズ \(n(x, t)\) の場合。
ラグランジュアプローチで推定される運きは
\[
\tilde{\delta}(t)=\frac{I_t^\prime}{I_x^\prime}=\frac{I_t+n_t}{I_x+n_x} \tag{26}
\]
ここで \(n_x = \partial n/\partial x\) かつ \(n_t = n(x, t)-n(x, 0)\) である。\((n_t, n_x)\) の \((0, 0)\)(ノイズゼロ)に関するテイラー展開と(18)を用いると、
\[
\tilde{\delta}(t)\approx \delta(t)+\frac{n_t}{I_x}-n_x\frac{I_t}{I_x^2}+\frac{1}{2}\delta^2(t)I_{xx} \tag{27}
\]
(27)を(16)に代入し、\(I\) の \(x + (1 +\alpha)\delta(t)\) についてのテイラー展開を用いると、
★式(28)のカッコの数が合わない(ので \(,t)\)を追加した・・・)
\[
\tilde{I}_L^\prime(x,t)\approx I\left(x+(1+\alpha)\delta(t),0\right)+(1+\alpha)I_x\left(\frac{n_t}{I_x}-n_x\frac{I_t}{I_x^2}+\frac{1}{2}\delta^2(t)I_{xx},t \right)+n \tag{28}
\]
(19)を再度用いて(1)を引くと、ノイズの関数としてのラグランジュ誤差 \(\varepsilon_L(n)\) は
\[
\varepsilon_L(n)\approx\left|(1+\alpha)n_t-(1+\alpha)n_x\delta(t)-\frac{1}{2}(1+\alpha)\delta^2(t)I_{xx}n_x+\frac{1}{2}(1+\alpha)\delta^2(t)I_{xx}I_x+n\right| \tag{29}
\]
オイラーアプローチでは、ノイズの多い動きの拡大されたシーケンスは
\[
\begin{align}
\tilde{I}_E^\prime(x,t) &=I^\prime(x,0)+(1+\alpha)I_t^\prime \\
\\
&=I(x,0)+(1+\alpha)(I_t+n_t)+n \tag{30}
\end{align}
\]
(24)式から(1)式を引くと、ノイズの関数としてのオイラー誤差 \(\varepsilon_E(n)\) は
\[
\varepsilon_E(n)\approx\left|(1+\alpha)n_t+\frac{1}{2}(1+\alpha)^2\delta^2(t)I_{xx}-\frac{1}{2}(1+\alpha)\delta^2(t)I_{xx}I_x+n\right| \tag{31}
\]
(29)式と(31)式でノイズをゼロに設定すると、結果として得られる誤差は(21)式と(24)式に示すようにノイズのない信号に対して導出された誤差に対応する。